Linear Parabolic Equations in 1 Dimension
This web application solves linear partial differential
equations in 1 dimension
using finite element and finite difference methods to approximate the solution in each case.
The Default method is the Implicit Finite Difference Method. One can also
use the Finite Element Method to solve these systems.
The Implicit Finite Difference Method is a numerical technique used to solve partial
differential equations (PDEs). Unlike the explicit finite difference method,
which calculates the solution at each time step based on the previous time step,
the implicit method considers the entire system of equations simultaneously.
The Finite Element Method is a numerical technique used to solve partial differential
equations (PDEs). It is based on the idea of dividing the domain into smaller, simpler
elements, and then approximating the solution within each element. The method is
particularly useful for solving problems with complex geometries or boundary conditions.
The implicit method is particularly useful when the output expression at a forward time step depends
on itself, and there are no restrictions on the time step. It handles cases where there are more than
one unknown in the finite difference equation
Just select the preferred
method from the Tools submenu.
For instance in order to solve a Linear Parabolic Equation on the interval
[A,B] from time t=s to t=T, we use the following template:
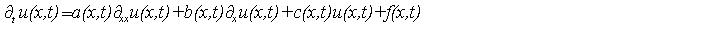
Click the enter button to fill in the coefficients and initial conditions and
the press the
solve button.
|
|