|
This web application solves various linear and nonlinear partial differential equations in
1, 2 and 3 dimensions
using finite element and finite difference methods to approximate the solution in each case.
The equations usually involve an unknown for fonction of more than two variables with its partial
derivatives. They have the following general form.
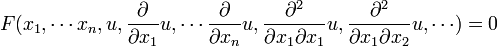
Partial differential equations are used in various scientific and engineering modeling and
analysis studies for research and development of new technologies.
Partial differential equations are ubiquitous in mathematically oriented scientific fields,
such as physics and engineering. For instance, they are foundational in the modern scientific
understanding of sound, heat, diffusion, electrostatics, electrodynamics, thermodynamics,
fluid dynamics, elasticity, general relativity, and quantum mechanics (Schrödinger equation,
Pauli equation etc.). They also arise from many purely mathematical considerations, such as
differential geometry, stochastic analysis and the calculus of variations; among other notable
applications, they are the fundamental tool in the proof of the Poincaré conjecture from geometric topology.
In this application, equations are mainly second order equations and can be classified as
Parabolic, Elliptic or Hyperbolic, and are defined using templates from the menu
above.
For instance in order to solve a Linear Parabolic Equation on the interval
[A,B] from time t=s to t=T, we use the following template:
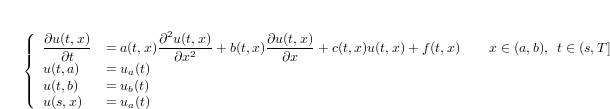
Click the enter button to fill in the coefficents and initial conditions and
then press the
solve button.
Note that this web application supports elementary functions, their syntax is
similar as in C++ math.h library, i.e. abs(x), sin(x), cos(x), exp(x), log(x), sqrt(x),
tan(x), acos(x), asin(x), atan(x),...etc.
|
|